Confirmatory factor analysis (CFA) is a special type of structural equation model in which a factor (or multiple factors) is represented by several indicator variables/measurements. The goal of CFA is to validate some hypothesized measurement model.
The general idea behind CFA is that we might believe a person possesses some underlying, immeasurable construct — say, math aptitude. Because we can’t directly measure math aptitude, we might give the person a math test that has several questions, and our hypothesis is that the questions on this test appropriately measure math aptitude. We then use CFA to confirm (hence the name!) that the items suitably measure this construct. We make claims about the appropriateness/goodness of the model by examining the factor loadings and fit statistics of the model.
Simplest Version
In the simplest version of a CFA model, we might have a short test that measures a single construct. In this simplest model, the test needs to comprise at least 3 items, otherwise the model will be underidentified and the parameters can’t be estimated.
But say we have a test of math aptitude that comprises 4 items. The assumption is that math aptitude “causes” (or “accounts for”) a considerable amount of the performance on each of these 4 items. Visually, the model looks like this:
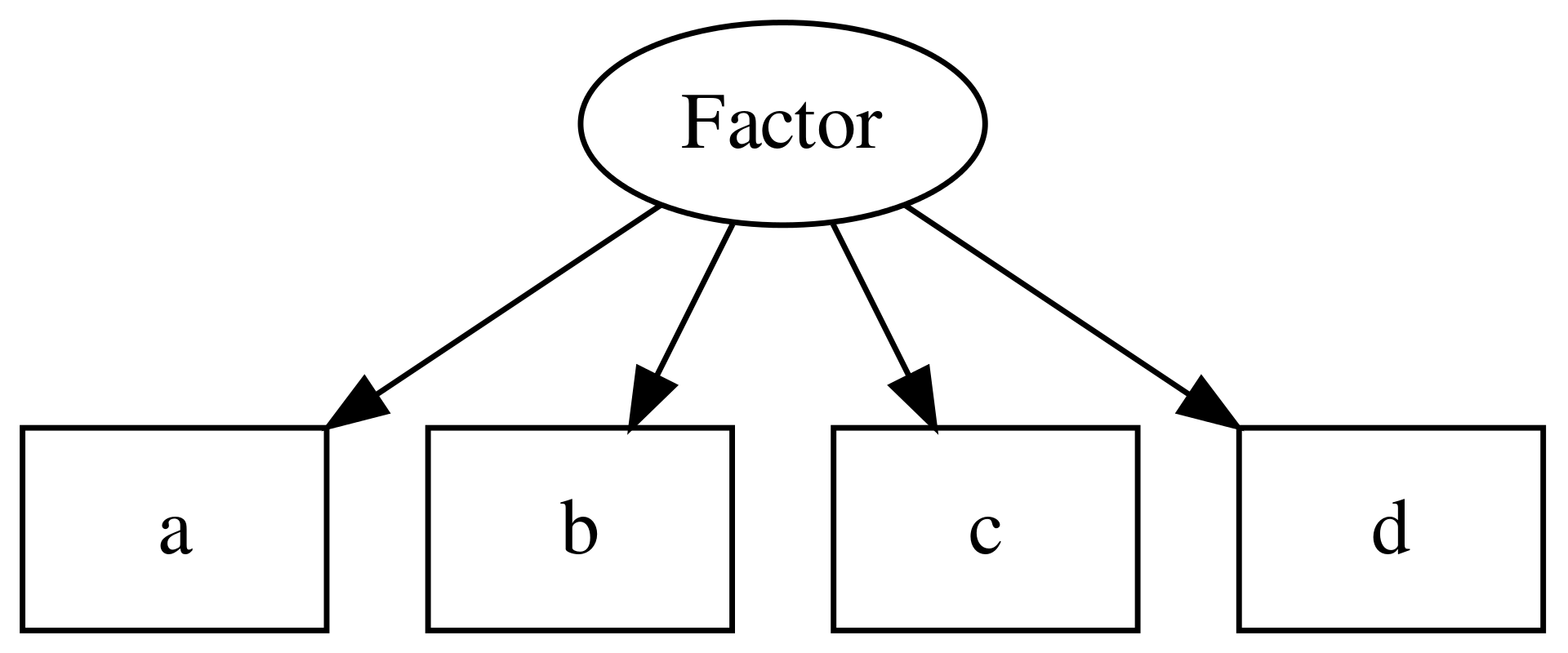
Where “factor” corresponds to math aptitude, and each of the rectangles represents an item on the math test. The arrows indicate that the factor “causes” scores on each of these test items.
This model also assumes that the items are conditionally independent. That is, after we take math aptitude into account, we’re hypothesizing no covariance between any of the items.
RESUME HERE…